Filtering Data with L2 Regularisation

I have just finished reading Momentum Strategies with L1 Filter by Tung-Lam Dao. The smoothing results presented in this paper are interesting and I thought it would be cool to implement the L1 and L2 filtering schemes in R. We’ll start with the L2 scheme here because it has an exact solution and I will follow up with the L1 scheme later on.

Formulation of the Problem

Consider some time series data consisting of \(n\) points, \(y_t = x_t + \epsilon_t\), where \(x_t\) is a smooth signal, \(\epsilon_t\) is noise and \(y_t\) is the combined noisy sign. If we have observations of \(y_t\), how can get back to an estimate of \(x_t\)?

The Hodrick-Prescott filter works by minimising the objective function

$$\frac{1}{2} \sum_{t=1}^n (y_t - x_t)^2 + \lambda \sum_{t=2}^{n-1} (x_{t-1} - 2 x_t + x_{t+1})^2.$$

The regularisation parameter, \(\lambda\), balances the contributions of the first and second summations, where the first is the sum of squared residuals and the second is the sum of squared curvatures in the filtered signal (characterised by the central difference approximation for the second derivative). A small value for \(\lambda\) causes the residuals to dominate the optimisation problem. A large value for \(\lambda\) will result in a solution which minimises curvature.

Implementation and Test Data

Implementing a function to perform the optimisation is pretty simple.

l2filter.optim <- function(x, lambda = 0.0) {
  objective <- function(y, lambda) {
    n <- length(x)
    
    P1 = 0.5 * sum((y - x)**2)
    #
    P2 = 0
    for (i in 2:(n-1)) {
      P2 = P2 + (y[i-1] - 2 * y[i] + y[i+1])**2
    }
    #
    P1 + lambda * P2
  }
  #
  optim(x, objective, lambda = lambda, method = "BFGS")$par
}

It has a nested objective function. The BFGS method is specified for optim() because the Nelder and Mead optimisation scheme converged too slowly.

First we’ll try this out on some test data.

N <- 20

set.seed(1)

(y <- 1:N + 10 * runif(N))

 [1]  3.6551  5.7212  8.7285 13.0821  7.0168 14.9839 16.4468 14.6080 15.2911 10.6179 13.0597
[12] 13.7656 19.8702 17.8410 22.6984 20.9770 24.1762 27.9191 22.8004 27.7745

If we use \(\lambda = 0\) then regularisation has no effect and the objective function is minimised when \(x_t = y_t\). Not surprisingly, in this case the filtered signal is the same as the original signal.

l2filter.optim(y, 0)

 [1]  3.6551  5.7212  8.7285 13.0821  7.0168 14.9839 16.4468 14.6080 15.2911 10.6179 13.0597
[12] 13.7656 19.8702 17.8410 22.6984 20.9770 24.1762 27.9191 22.8004 27.7745

If, on the other hand, we use a large value for the regularisation parameter then the filtered signal is significantly different.

l2filter.optim(y, 100)

 [1]  5.8563  7.0126  8.1579  9.2747 10.3484 11.3835 12.3677 13.3067 14.2269 15.1607 16.1463
[12] 17.1989 18.3183 19.4873 20.6963 21.9274 23.1729 24.4203 25.6621 26.9082

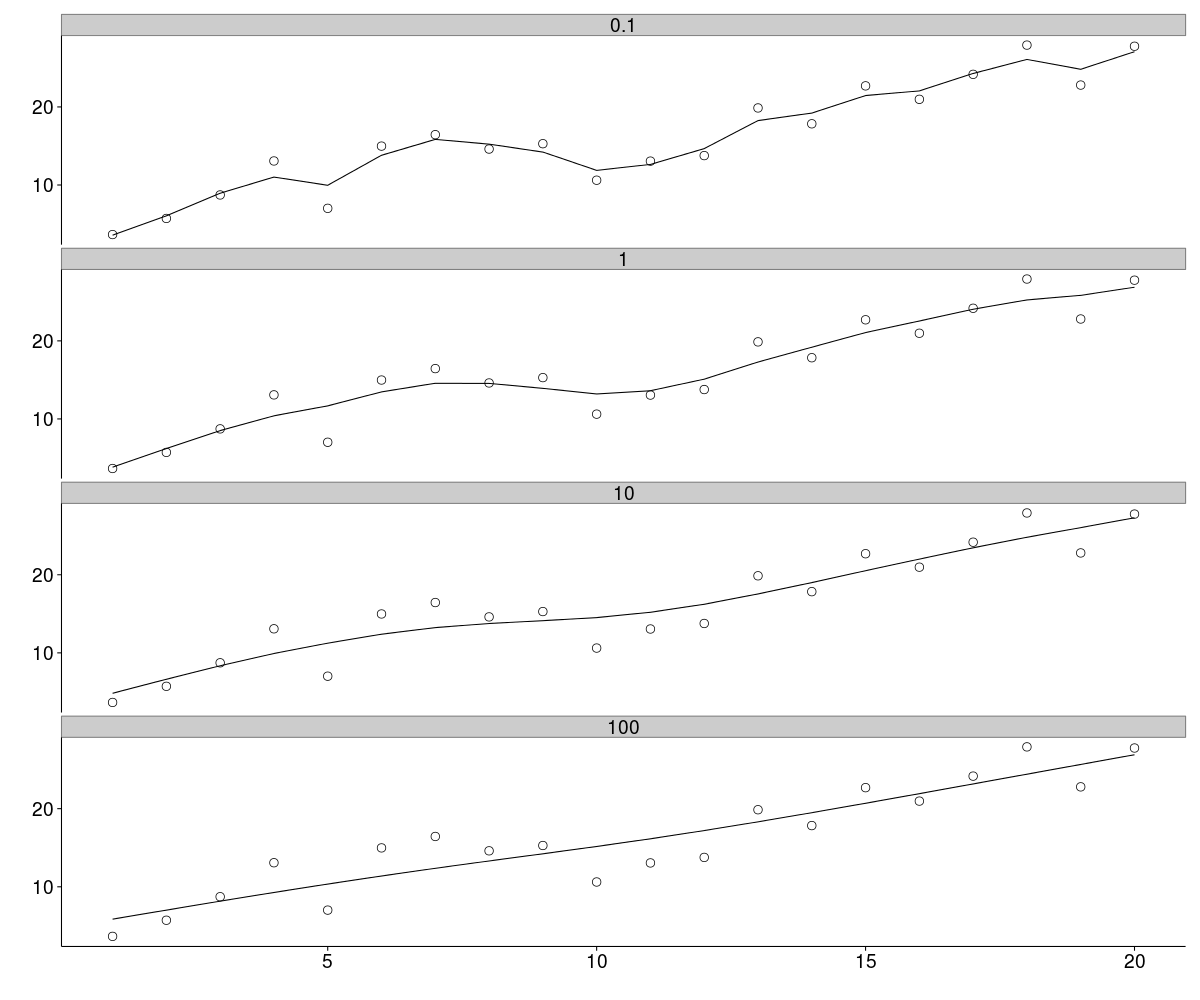
A plot is the most sensible way to visualise the effects of \(\lambda\). Below the original data (circles) are plotted along with the filtered data for values of \(\lambda\) from 0.1 to 100. In the top panel, weak regularisation results in a filtered signal which is not too different from the original. At the other extreme, the bottom panel shows strong regularisation where the filtered signal is essentially a straight line (all curvature has been removed). The other two panels represent intermediate levels of regularisation and it is clear how the original signal is being smoothed to varying degrees.

Matrix Implementation

As it happens there is an exact solution to the Hodrick-Prescott optimisation problem, which involves some simple matrix algebra. The core of the solution is a band matrix with a right bandwidth of 2. The non-zero elements on each row are 1, -2 and 1. The function below constructs this matrix in a rather naive way. However, it is simply for illustration: we will look at a better implementation using sparse matrices.

l2filter.matrix <- function(x, lambda = 0.0) {
  n <- length(x)
  
  I = diag(1, nrow = n)
  
  D = matrix(0, nrow = n - 2, ncol = n)
  #
  for (i in 1:(n-2)) {
    D[i, i:(i+2)] = c(1, -2, 1)
  }
  
  c(solve(I + 2 * lambda * t(D) %*% D) %*% x)
}

Applying this function to the same set of test data, we get results consistent with those from optimisation.

l2filter.matrix(y, 100)

 [1]  5.8563  7.0126  8.1579  9.2747 10.3484 11.3835 12.3677 13.3067 14.2269 15.1607 16.1463
[12] 17.1989 18.3183 19.4873 20.6963 21.9274 23.1729 24.4203 25.6621 26.9082

In principle the matrix solution is much more efficient than the optimisation. However, an implementation using a dense matrix (as above) would not be feasible for a data series of any appreciable length due to memory constraints. A sparse matrix implementation does the trick though.

library(Matrix)

l2filter.sparse <- function(x, lambda = 0.0) {
  n <- length(x)
  
  I = Diagonal(n)
  
  D = bandSparse(n = n - 2, m = n, k = c(0, 1, 2),
                 diagonals = list(rep(1, n), rep(-2, n), rep(1, n)))
  
  (solve(I + 2 * lambda * t(D) %*% D) %*% x)[,1]
}

Again we can check that this gives the right results.

l2filter.sparse(y, 100)

 [1]  5.8563  7.0126  8.1579  9.2747 10.3484 11.3835 12.3677 13.3067 14.2269 15.1607 16.1463
[12] 17.1989 18.3183 19.4873 20.6963 21.9274 23.1729 24.4203 25.6621 26.9082

Application: S&P500 Data

Let’s take this out for a drive in the real world. We’ll get out hands on some S&P500 data from Quandl.

library(Quandl)

Quandl.auth("xxxxxxxxxxxxxxxxxxxx")

SP500 = Quandl("YAHOO/INDEX_GSPC", start_date = "1994-01-01", end_date = "2014-01-01")
#
SP500 = SP500[, c(1, 5)]

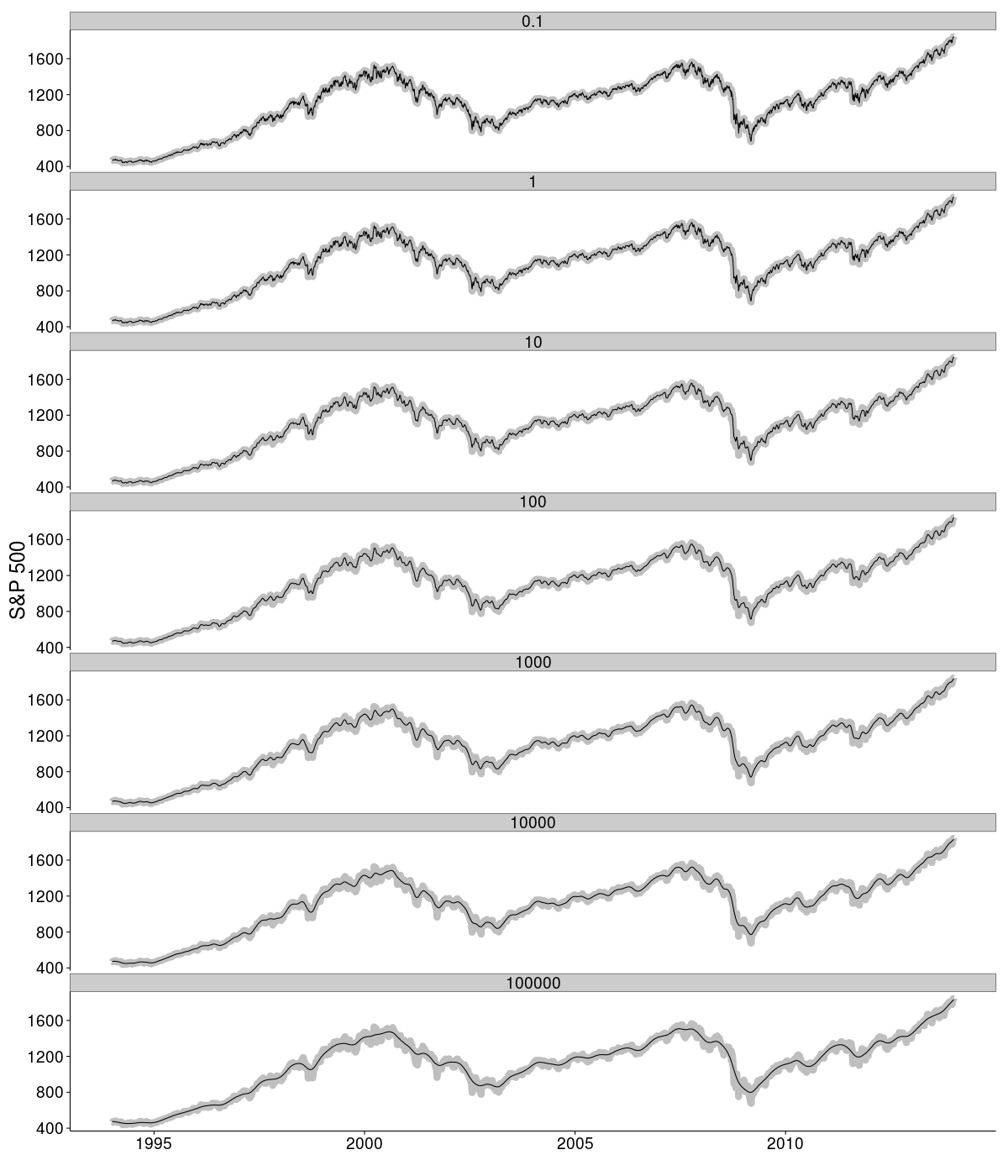
Then systematically apply the filter with a range of regularisation parameters scaling from 0.1 to 100000 in multiples of 10. The results are plotted below. In each panel the grey data reflect the raw daily values for the S&P500 index. Superimposed on top of these are the results of filtering the signal using the specified regularisation parameter. As anticipated, larger values of \(\lambda\) result in a smoother curve since the filter is more heavily penalised for curvature in the filtered signal.

I think that the results look rather compelling. The only major drawback to this filter seems to be the fact, if used dynamically, the algorithm can (and most likely will) cause previous states to change. If used, for example, as the basis for an indicator on a chart, this would cause repainting of historical values.