
The packages we’ll be looking at today should bring joy to the hearts of all Physical Scientists. Actually they should make any flavour of Scientist happy.
It is natural for man to relate the units of distance by which he travels to the dimensions of the globe that he inhabits. Thus, in moving about the earth, he may know by the simple denomination of distance its proportion to the whole circuit of the earth. This has the further advantage of making nautical and celestial measurements correspond. The navigator often needs to determine, one from the other, the distance he has traversed from the celestial arc lying between the zeniths at his point of departure and at his destination. It is important, therefore, that one of these magnitudes should be the expression of the other, with no difference except in the units. But to that end, the fundamental linear unit must be an aliquot part of the terrestrial meridian. ... Thus, the choice of the metre was reduced to that of the unity of angles. Pierre-Simon Laplace
SIUnits
The SIUnits package provides unit-checked operations for quantities expressed in SI units.
using SIUnits
using SIUnits.ShortUnits
It supports both long and short forms of units and all the expected arithmetic operations.
1KiloGram + 2kg
3 kg
4Meter - 2m
2 m
4m / 2s
2.0 m s⁻¹
Note that it only recognises the American spelling of “meter” and not the (IMHO correct) “metre”! But this is a small matter. And I don’t want to engage in any religious wars.
Speaking of small matters, it’s possible to define new units of measure. Below we’ll define the micron and Angstrom along with their conversion functions.
import Base.convert
Micron = SIUnits.NonSIUnit{typeof(Meter),:µm}()
µm
convert(::Type{SIUnits.SIQuantity},::typeof(Micron)) = Micro*Meter
convert (generic function with 461 methods)
Angstrom = SIUnits.NonSIUnit{typeof(Meter),:Å}()
Å
convert(::Type{SIUnits.SIQuantity},::typeof(Angstrom)) = Nano/10*Meter
convert (generic function with 462 methods)
And now we can freely use these new units in computations.
5Micron
5 µm
1Micron + 1m
1000001//1000000 m
5200Angstrom # Green light
5200 Å
Read on below to find out about the Physical package.
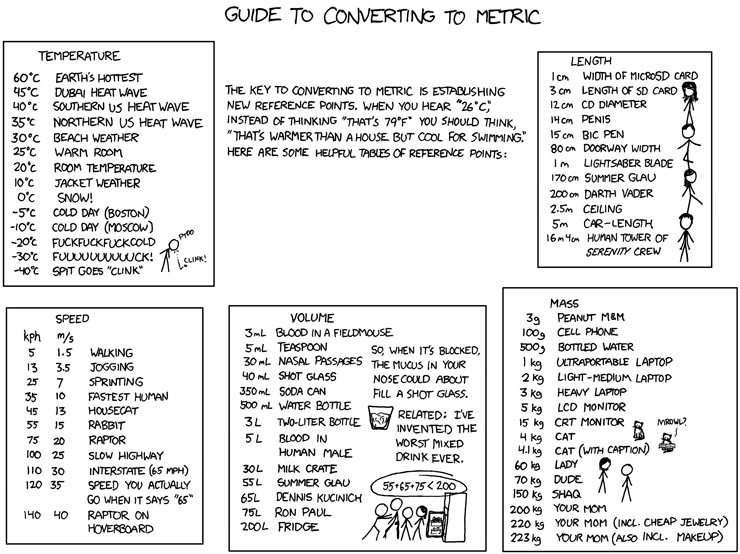
Physical
The Physical package is documented here. Apparently it’s not as performant as SIUnits but it does appear to have a wider scope of functionality. We’ll use it to address an issue raised on Day 17: converting between Imperial and Metric units.
Let’s kick off by loading the package.
using Physical
There’s a lot of functionality available, but we are going to focus on just one thing: converting pounds and inches into kilograms and metres. First we define a pair of derived units. To do this, of course, we need to know the appropriate conversion factors!
Inch = DerivedUnit("in", 0.0254*Meter)
1 in
Pound = DerivedUnit("lb", 0.45359237*Kilogram)
1 lb
We can then freely change the average heights and weights that we saw earlier from Imperial to Metric units.
asbase(66Inch)
1.6764 m
asbase(139Pound)
63.04933943 kg
On a related note I’ve just put together a package of physical constants for Julia.
using PhysicalConstants
PhysicalConstants.MKS.SpeedOfLight
2.99792458e8
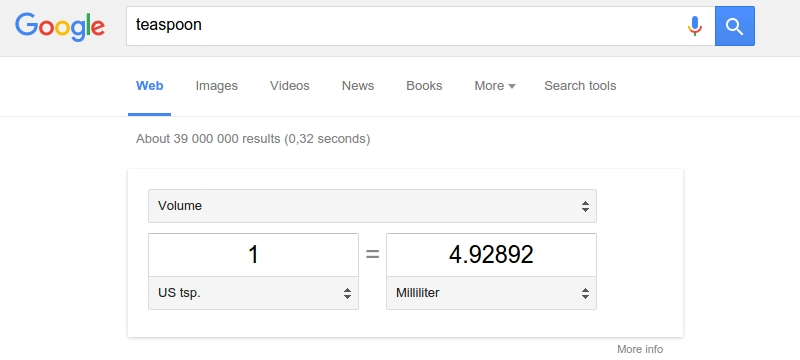
PhysicalConstants.MKS.Teaspoon
4.92892159375e-6
Did you know that a teaspoon was 4.92892 millilitres? There I was, wallowing in my ignorance, thinking that it was 5 millilitres. Pfffft. Silly me.
Units can be a contentious issue. Watch the video below to see what Richard Feynman had to say about the profusion of units used by Physicists to measure energy. Also check out the full code for today along with the index to the entire series of #MonthOfJulia posts on GitHub.
For those who want some proof that physicists are human, the proof is in the idiocy of all the different units which they use for measuring energy. Richard P. Feynman