
Today we’re going to look at the Clustering package, the documentation for which can be found here. As usual, the first step is loading the package.
using Clustering
We’ll use the RDatasets package to select the xclara data and rename the columns in the resulting data frame.
using RDatasets
xclara = dataset("cluster", "xclara");
names!(xclara, [symbol(i) for i in ["x", "y"]]);
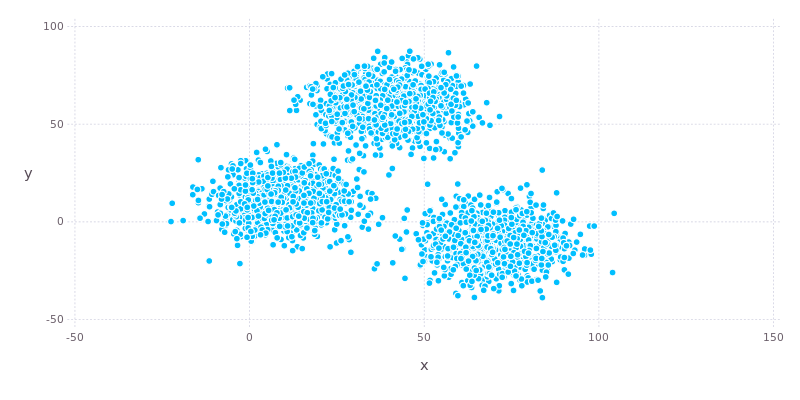
Using Gadfly to generate a plot we can clearly see that there are three well defined clusters in the data.
Next we need to transform the data into an Array and then transpose it so that each point lies in a separate column (remember that this is key to calculating distances!).
xclara = convert(Array, xclara);
xclara = xclara';
Before we can run the clustering algorithm we need to identify seed points which act as the starting locations for clusters. There are a number of options for doing this. We’re simply going to choose three points in the data at random. How did we arrive at three starting points (as opposed to, say, six)? Well, in this case it was simply visual inspection: there appear to be three clear clusters in the data. When the data are more complicated (or have higher dimensionality) then choosing the number of clusters becomes a little more tricky.
initseeds(:rand, xclara, 3)
3-element Array{Int64,1}:
2858
980
2800
Now we’re ready to run the clustering algorithm. We’ll start with k-means clustering.
xclara_kmeans = kmeans(xclara, 3);
A quick plot will confirm that it has recognised the three clusters that we intuitively identified in the data.

We can have a look at the cluster centers, the number of points assigned to each cluster and (a subset of) the cluster assignments.
xclara_kmeans.centers
2x3 Array{Float64,2}:
9.47805 69.9242 40.6836
10.6861 -10.1196 59.7159
xclara_kmeans.counts
3-element Array{Int64,1}:
899
952
1149
xclara_kmeans.assignments[1:10]
10-element Array{Int64,1}:
2
2
2
2
2
2
2
2
2
2
The k-means algorithm is limited to using the Euclidean metric to calculate the distance between points. An alternative, k-medoids clustering, is also supported in the Clustering package. The kmedoids() function accepts a distance matrix (from an arbitrary metric) as it’s first argument, allowing for a far greater degree of flexibility.
The final algorithm implemented by Clustering is DBSCAN, which is a density based clustering algorithm. In addition to a distance matrix, dbscan() also requires neighbourhood radius and the minimum number of points per cluster.
using Distances
dclara = pairwise(SqEuclidean(), xclara);
xclara_dbscan = dbscan(dclara, 10, 40);
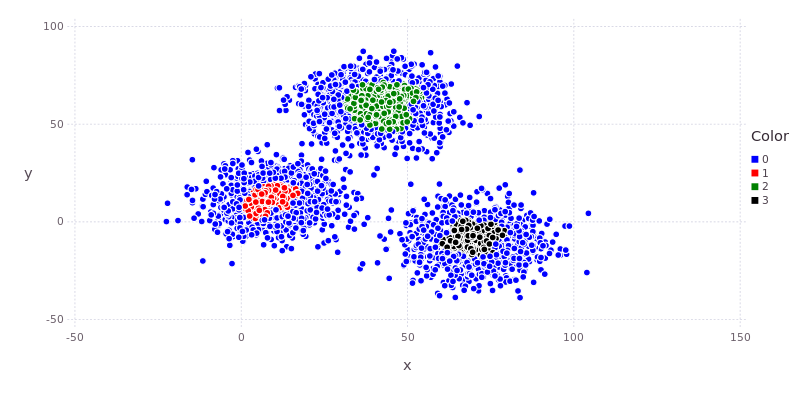
As is apparent from the plot below, DBSCAN results in a dramatically different set of clusters. The loosely packed blue points on the periphery of each of the three clusters have been identified as noise by the DBSCAN algorithm. Only the high density cores of these clusters are now separately identified.
That’s it for the moment about clusters. The full code for today can be found on github. Tomorrow we’ll take a look at regression. In the meantime, take a few minutes to watch the video below about using Julia’s clustering capabilities for climate classification.