
Is this a “good” model? How to validate a model and determine whether it’s a good representation of the training data and likely to produce robust and reliable predictions.
Create a model for the Tata Steel returns.
specification <- ugarchspec(
mean.model = list(armaOrder = c(0, 0)),
variance.model = list(model = "gjrGARCH"),
distribution.model = "std"
)
fit <- ugarchfit(data = TATASTEEL, spec = specification)
Check 1: Standardised Returns
📢 The standardised residuals should have a mean close to 0 and a standard deviation close to 1.
Calculate the mean and standard deviation of the residuals:
mean(residuals(fit, standardize=TRUE))
[1] 0.01247962
sd(residuals(fit, standardize=TRUE))
[1] 0.9924989
Those are both close to the target values. Good start!
Check 2: Constant Variability of Standardised Returns
📢 The standardised returns have uniform variability.
First look at the original returns.
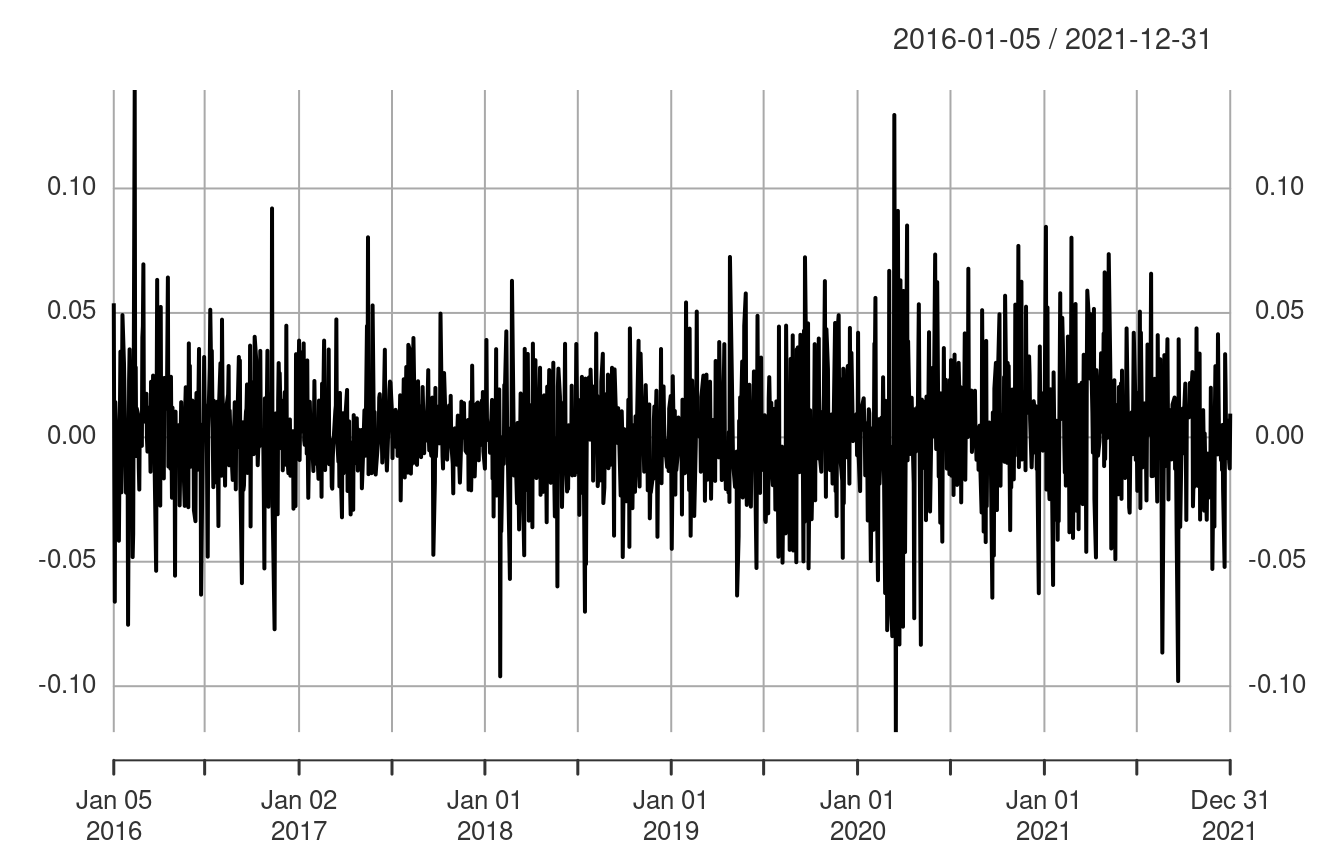
Compare to the returns standardise by the GARCH variability.
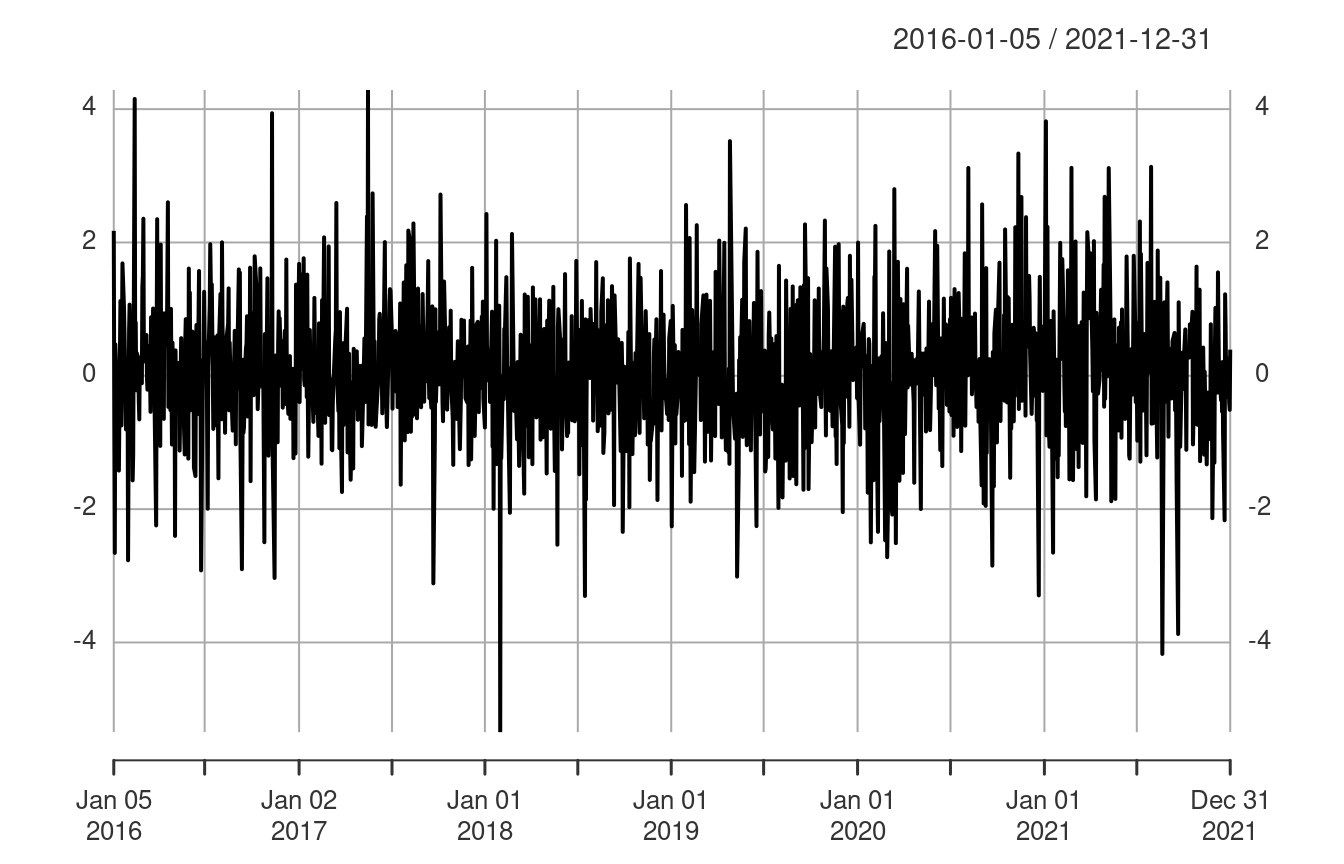
The standardised returns still have spikes, but the variability is more consistent and there is less evidence of volatility clustering.
Check 3: Autocorrelations
📢 The standardised returns have uniform variability.
Take a look at the correlogram of the absolute returns.
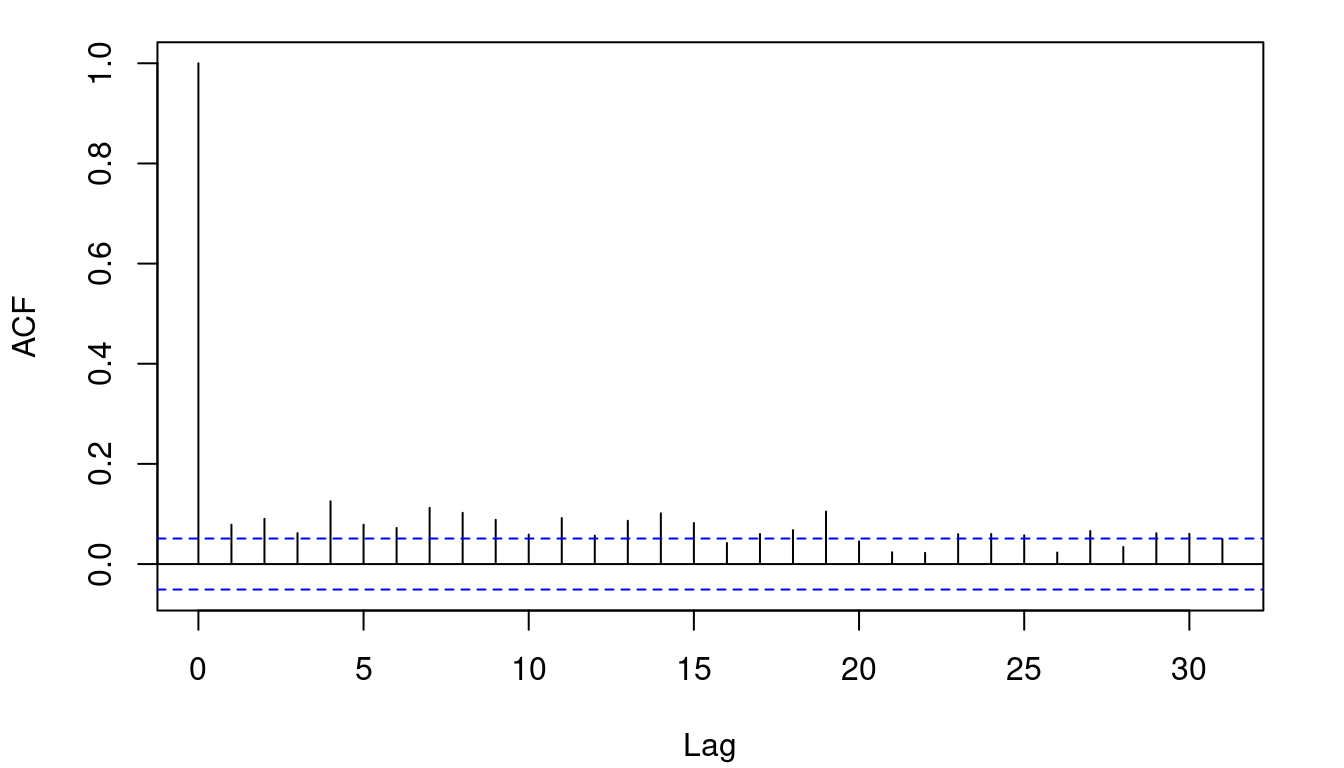
As expected, the autocorrelation is maximum at zero lag. However there is a long tail of significant autocorrelations at greater lags.
Now consider the correlogram of the absolute standardised returns.
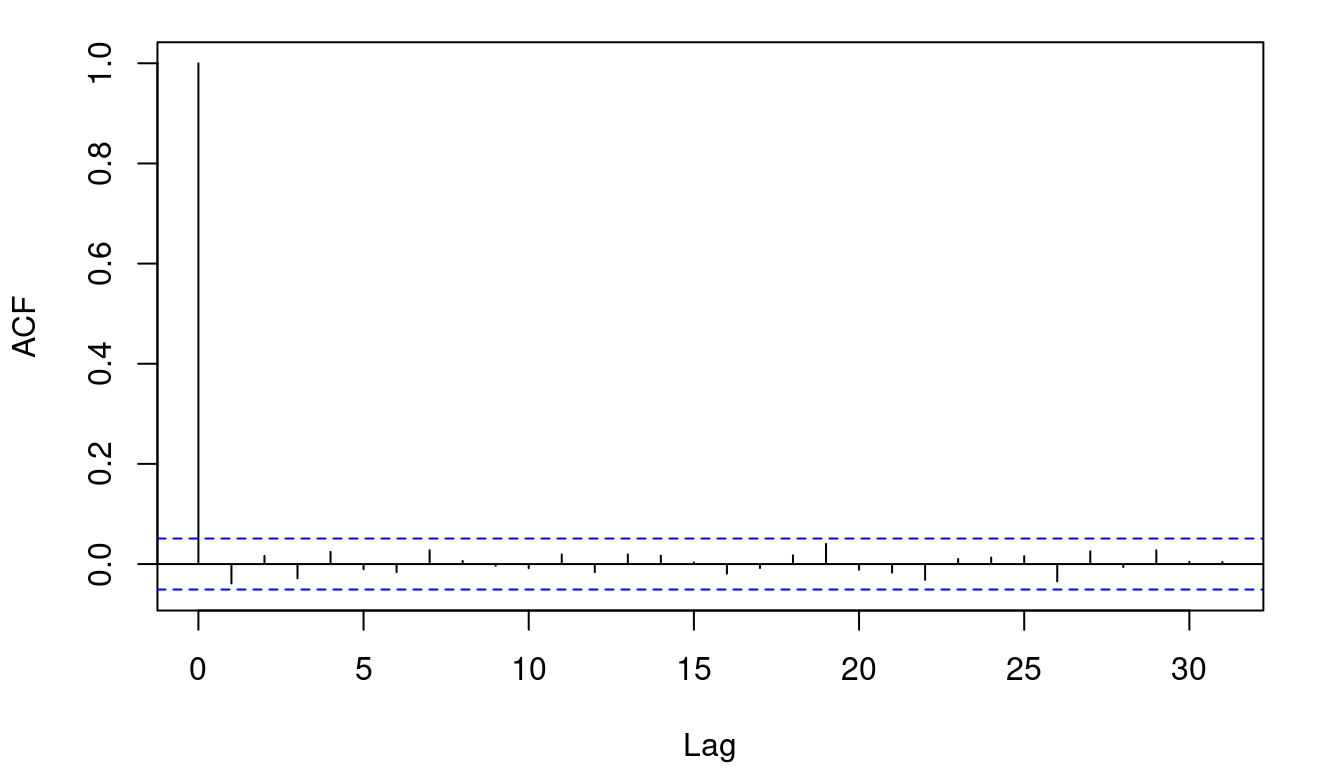
The only significant autocorrelation occurs at lag 0, which is precisely what we want: no lagged autocorrelation.
A qualitative comparison is a good start. But we can formalise this using a Ljung-Box test, which is a statistical test to determine whether autocorrelations are significantly different from zero. The null hypothesis for this test is that the data are not autocorrelated.
First apply the test to the absolute residuals.
Box.test(abs(residuals(fit)), 30, type = "Ljung-Box")
Box-Ljung test
data: abs(residuals(fit))
X-squared = 245.09, df = 30, p-value < 2.2e-16
The tiny \(p\)-value indicates a statistically significant result. We can this reject the null hypothesis and conclude that the data are autocorrelated.
Now let’s apply the test to the absolute standardised residuals.
Box.test(abs(residuals(fit, standardize=TRUE)), 30, type = "Ljung-Box")
Box-Ljung test
data: abs(residuals(fit, standardize = TRUE))
X-squared = 18.982, df = 30, p-value = 0.9404
Now the \(p\)-value is close to 1 and the result is certainly not statistically significant. We cannot rejected the null hypotheses. Although we cannot conclusively state that there is autocorrelation, it does seem unlikely given the test result.
Conclusion
These are three simple tests that can be applied to a model to assess its validity. All of these tests are, however, based on in sample data. A more definitive result would be based on using the model on unseen (out of sample) data.