
The distances of Hasler kayak races for various divisions are nominally 4, 8 and 12 miles. However, the actual distances vary to some degree from one race venue to another. This makes it difficult to compare race times across different races. Using data from Paddle UK I attempt to estimate the actual distances.
Background
In Hasler races paddlers are grouped according to division. Divisions range from 9 (lowest) to 1 (highest) and reflect the paddler’s (K1) or paddlers’ (K2) ability. The distance of the race depends on the division:
- 4 miles (divisions 7, 8 and 9)
- 8 miles (divisions 4, 5 and 6) and
- 12 miles (divisions 1, 2 and 3).
These are the nominal distances. In practice the distances may be somewhat longer or shorter from one venue to another.
In addition to paddling further, paddlers in higher divisions also have to contend with one (divisions 4, 5 and 6) or two (divisions 1, 2 and 3) portages.
The Data
The data used in this post was scraped from Paddle UK. The scraped data are available here. Incidentally, these data were mentioned in Data is Plural newsletter on 30 April 2025.

Wrangling
I imported the JSON version of the data and then did the following:
- selected only results for Hasler races;
- converted the race time to decimal hours;
- added a
typefield (K1 or K2) based on the race category; and - merged in a column for race distance.
Here’s a random sample of 10 rows from the resulting data.
race type division time distance
1 Pangbourne K1 7 0.6197222 4
2 Cambridge K2 9 0.6466667 4
3 Bishop's Stortford K1 6 1.3344444 8
4 Wey K1 6 1.3500000 8
5 Banbury K2 7 0.6836111 4
6 Chelmer K2 7 0.6677778 4
7 Maidstone K1 7 0.8783333 4
8 Leighton Buzzard K2 7 0.7105556 4
9 Pangbourne K1 6 1.4230556 8
10 Pangbourne K1 5 1.3394444 8
The first record, for example, reflects a finish time of around 0.6 hours (close to 37 minutes to be more precise) for a K1 competing in Division 7 at the Pangbourne Hasler. The nominal distance over which this paddler raced was 4 miles.
Corrected Distances
To estimate the distance correction I did the following:
- Calculate the average race time per race and nominal distance. This step aggregated results from multiple years. For example, the times for the Pangbourne Hasler in 2022, 2023 and 2024 were all included in the same average. This assumed that the race course at Pangbourne remained the same over those three years and that other factors (like weather or flow rate on the day) did not have a substantial impact on the race times. I’ll refer to this average as the race time.
- Calculate the average race time per distance. This is similar to the previous step but ignores the individual races, effectively assuming that the distances are consistent between venues. I’ll refer to this average as the global time.
- Calculate the correction factors as the ratios of the race times to the global times.
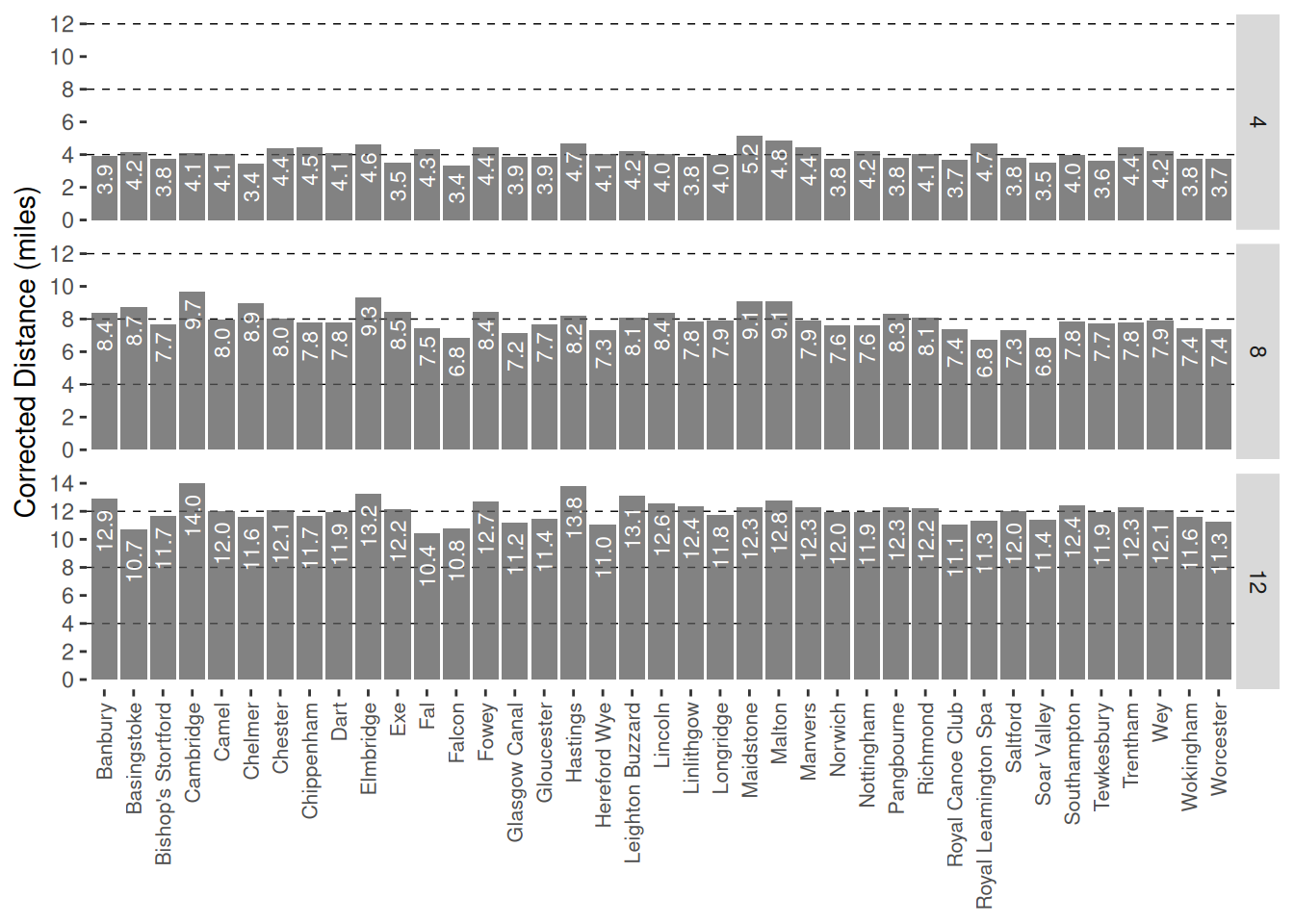
The correction factors were then used to generate corrected distances for each of the races by scaling the nominal distances. The plot below shows the corrected distances (along the vertical axis) broken down by race (along the horizontal axis) and nominal distance (the three panels).
Uncorrected Speeds
The primary reason for estimating the corrected distances was that the speeds calculated using the race times and nominal distances did not look realistic. The distribution of speeds plotted below below should help to illustrate the problem. I was compelled to convert from miles to km to calculate speeds in sensible (metric!) units.
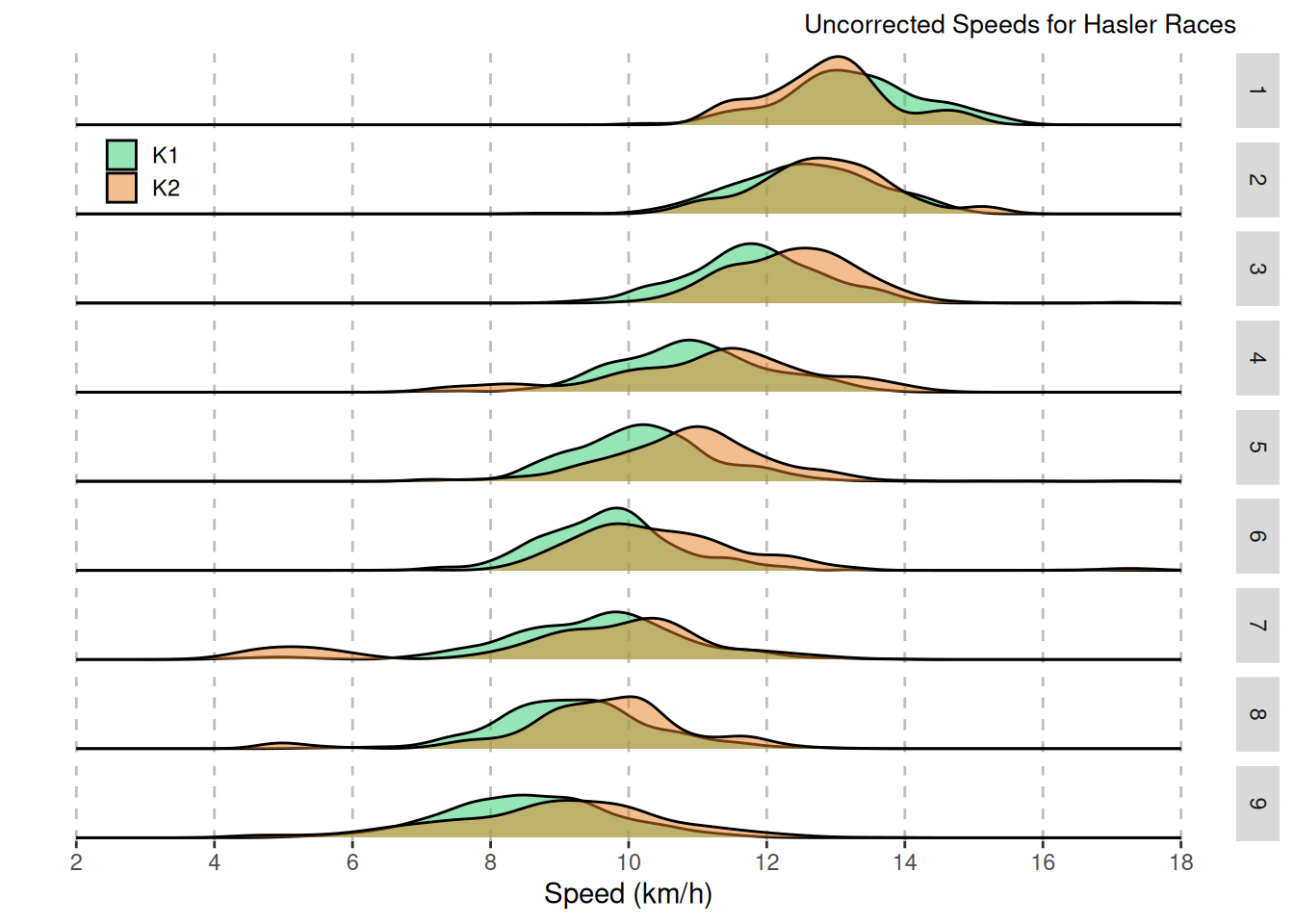
The speeds increase from Division 9 to Division 1 as expected. And for any given division the K2 speeds are generally higher than the corresponding K1 speeds (also as expected!). However, the dispersion of speeds is much larger than anticipated. I would have thought that within any one division there would be a much narrowed clustering of speeds. The increase in dispersion is due to varying distances between venues.
Corrected Speeds
But since we have calculated the corrected distances we can also calculate the corrected speeds.
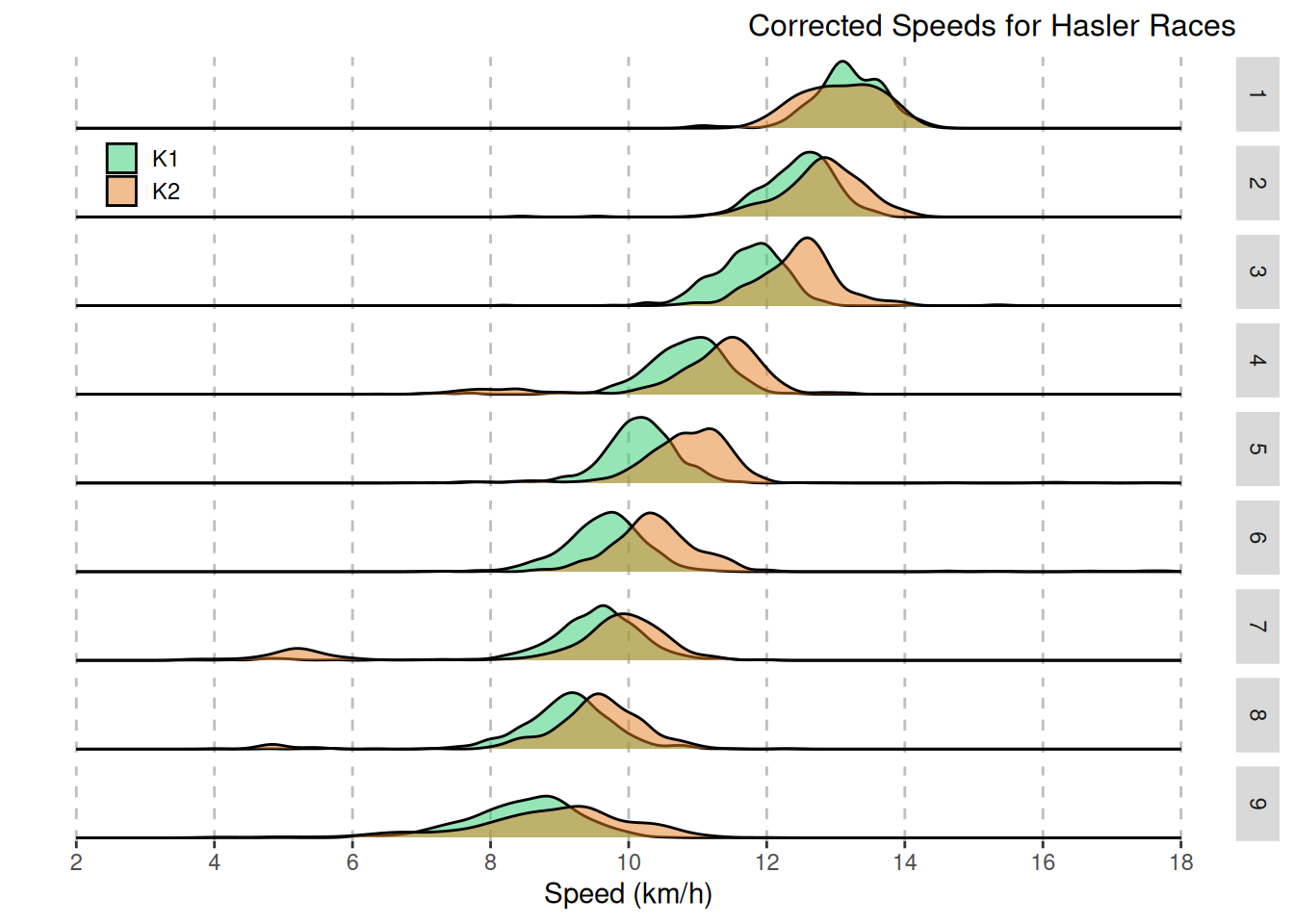
Now the speeds are more tightly clustered. This is consistent with my gut expectation for the speeds in each division.
It’s important to bear in mind that speeds have been used implicitly in calculating the corrected distances. However, given that there was aggressive averaging in the calculation of those distances I’m not too concerned about bias. Perhaps I’m underestimating the potential impact? Despite this concern I think that these are interesting results.